Research within DAE - our methods
Multi-scale problems are omnipresent in engineering and science, e.g.
- composite materials
- crystalline materials (metals, eramics)
- micro-defects (cracks, pores)
Understanding the relation between small-scale structures, the local mechanisms and the overall response of micro-heterogeneous structures is a key interst in our research. Visit our research projects to learn more about our activities. If you interested in a student research project, follow this link.
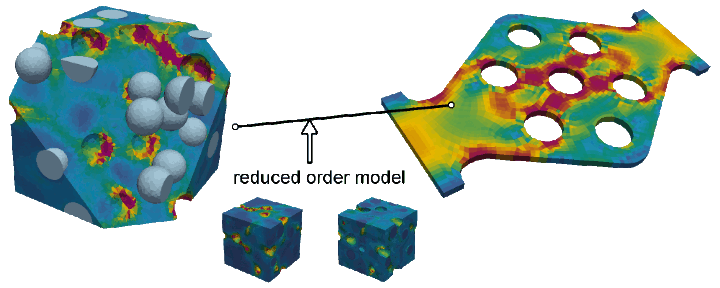
Reduced order models have been a focus in our research for years. In particular, our research portfolio comprises ROM for
- dissipative nonlinear multi-scale problems
- cyclic problems
- nonlinear hyperelasticity
- reduced cubature schemes using dictionary learning
- and materials including nonlinear interfaces.
Visit our research projects to learn more about our activities. If you interested in a student research project, follow this link.
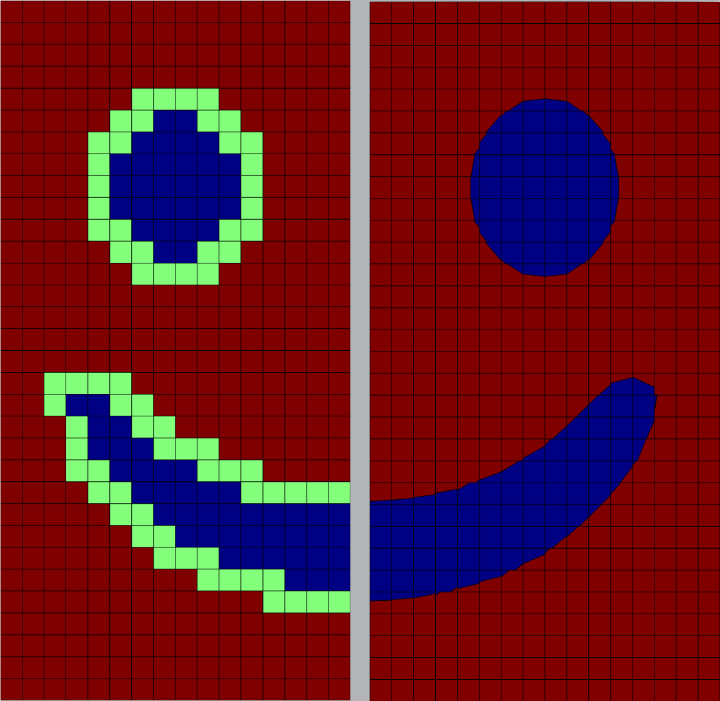
The use of the Fast Fourier Transform (FFT) has developed rapidly in the past three decades. Our team is contributing via
- massively parallel implementations
- interface considerations within FFT based models
- multi-phasic composite voxels
- rapid numerical schemes
Visit our research projects to learn more about our activities. If you interested in a student research project, follow this link.
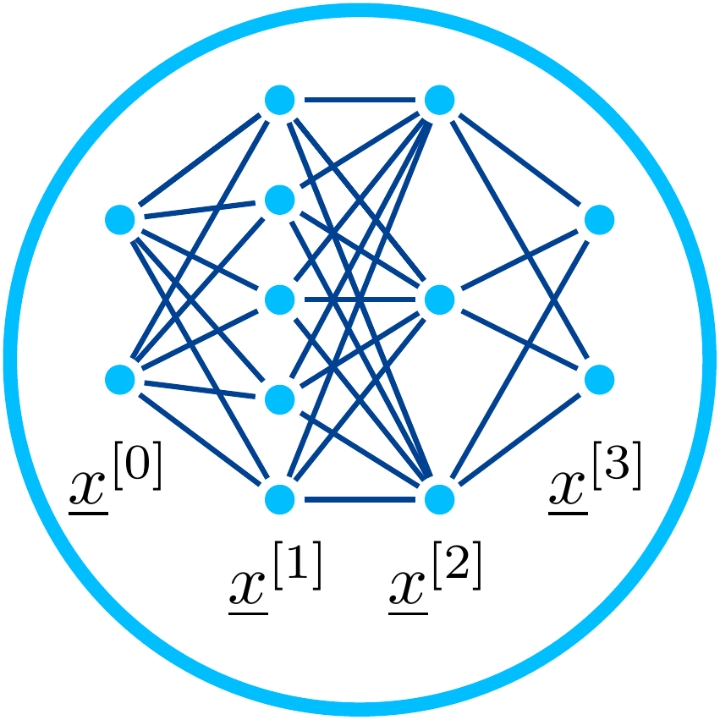
Machine learning is used in several projects (e.g. in PN3-1, PN3A-2). Our focus is on using physics in combination with machine learning. The research comprises
- image processing
- feature engineering
- property preserving machine learning
- dictionary learning
- data-supported cubature
- ...
Visit our research projects to learn more about our activities. If you interested in a student research project, follow this link.
The use of dedicated material models is the cornerstone of any advanced engineering simulation. Using physically and mathematically sound models is crucial. The models are put to life by using numerical models and by investigating the properties of models and their mathematical framework in a rigorous way. Our studies include but are not limited to
- two-point statistics of heterogeneous materials
- mathematical and numerical tools in material modeling
- variational formulations
- ...
Visit our research projects to learn more about our activities. If you interested in a student research project, follow this link.