Data-supported simulation and surrogate modeling of mechanical systems

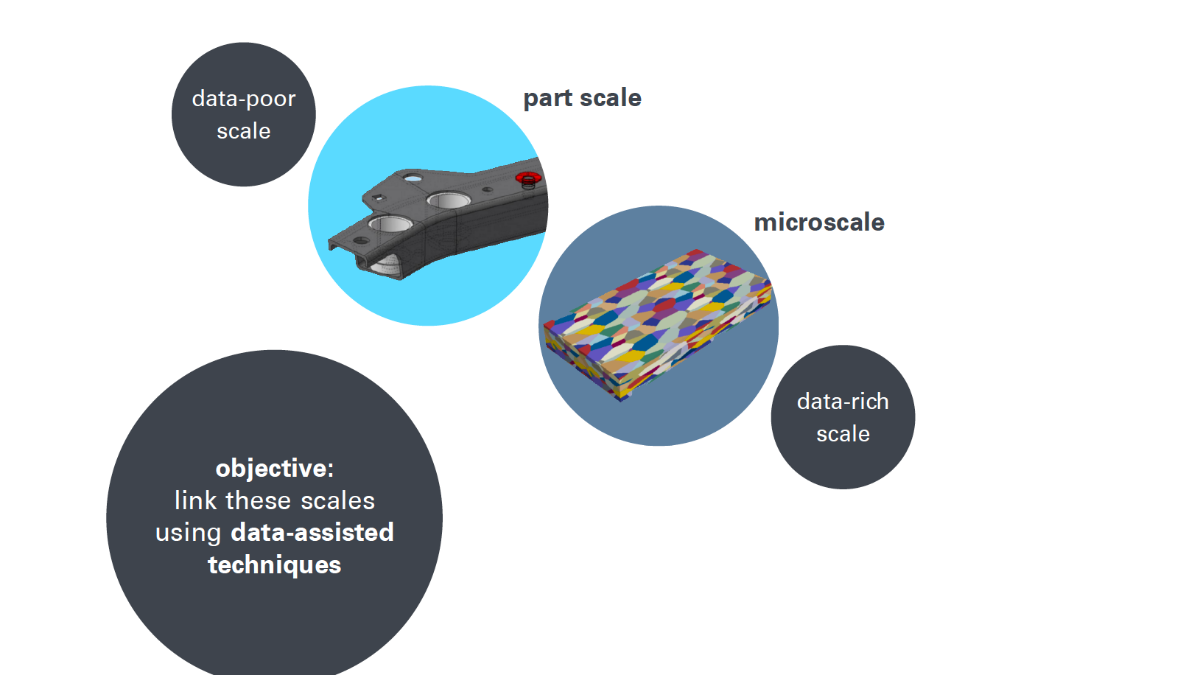
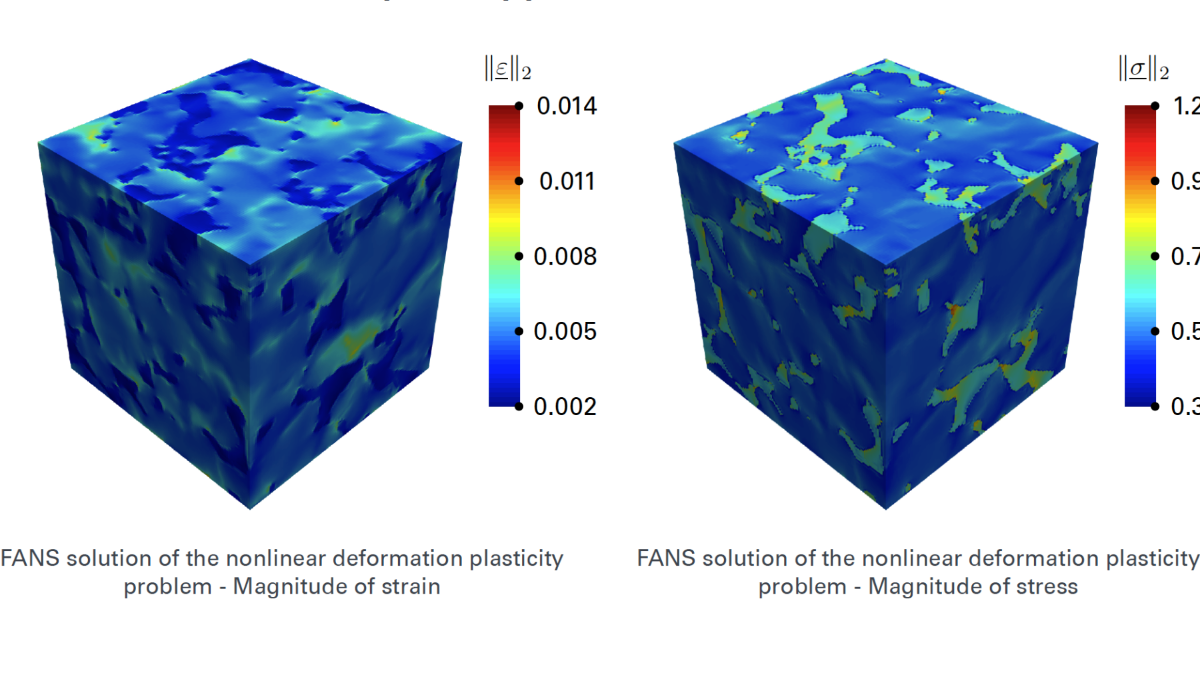
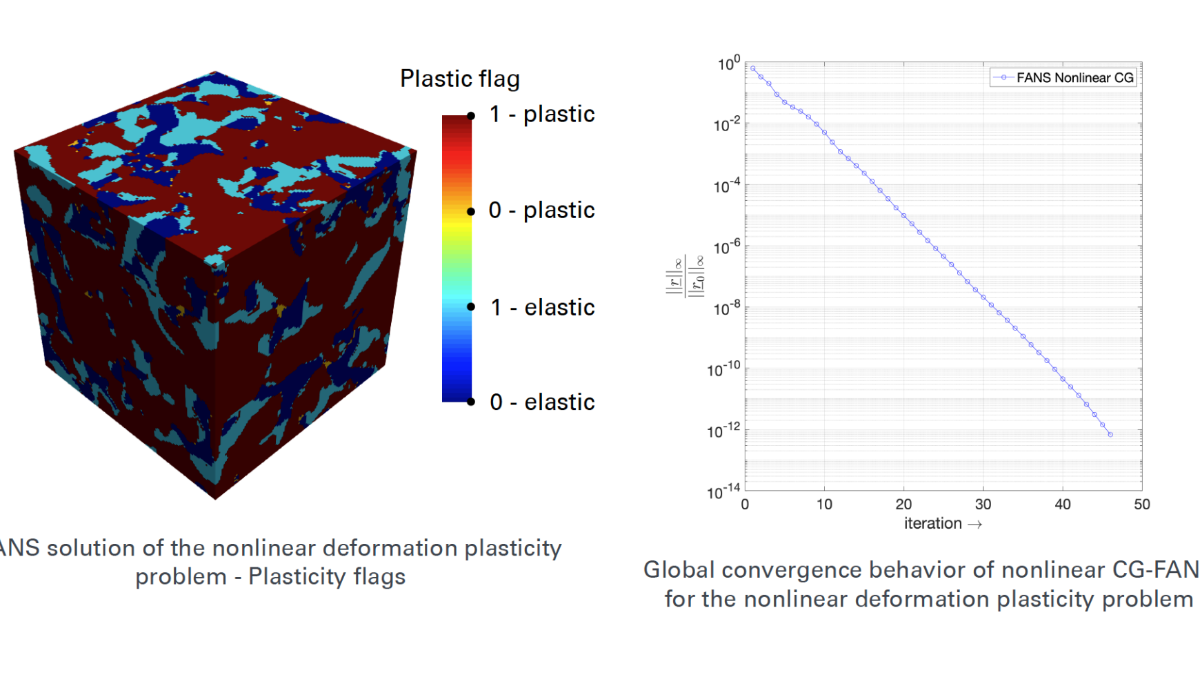
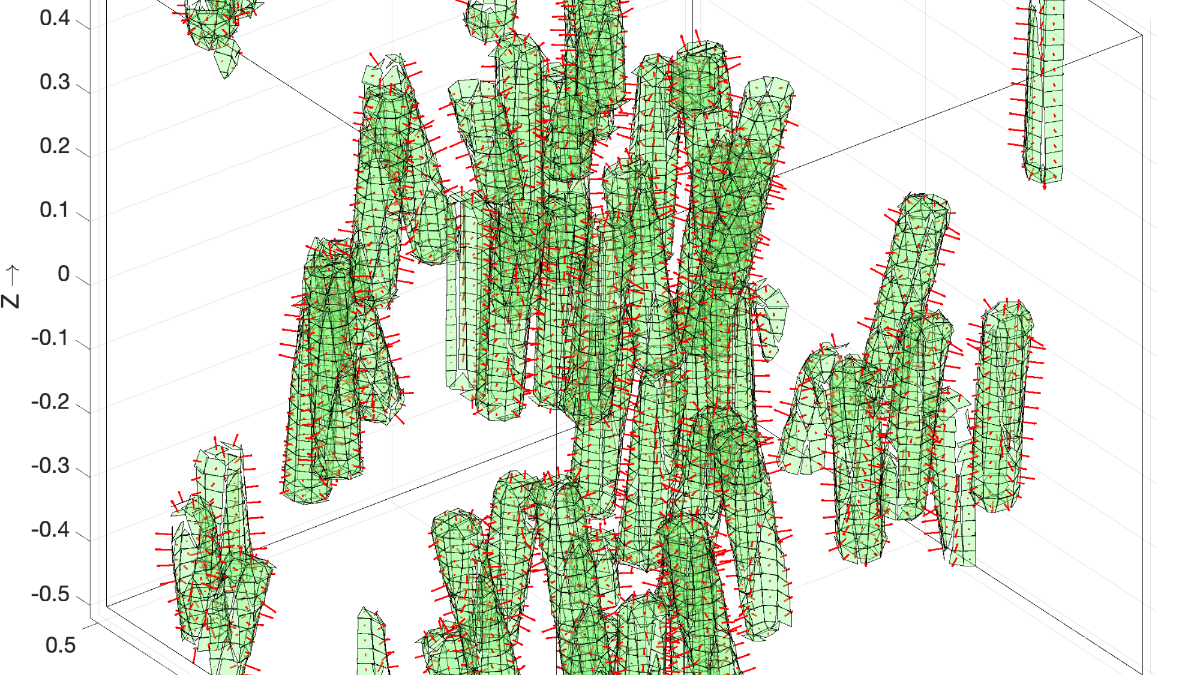
The majority of the materials that surround us are heterogeneous. In recent years, computational homogenization techniques have helped perform concurrent multi-scale simulations in the view of scale-bridging applications. For discrete and voxelized microstructural data, computational homogenization has become the gold standard to perform high-fidelity multi-scale analysis despite some disadvantages close to material boundaries. The massive computational complexity of simulations operating on such voxelized data comprising billions of unknowns induces the need for algorithmically and numerically highly efficient solvers at the microscale. In this project, we use a specific Fast Fourier Transform (FFT) based technique called Fourier accelerated nodal solvers (FANS) to efficiently perform numerical homogenization of heterogeneous microstructures for linear and nonlinear, thermal, mechanical and multi-physical problems operating on high-resolution regular grids. A hybrid (MPI + OpenMP) parallel implementation tool will be created to provide high-fidelity direct numerical simulations for linear and nonlinear problems on the microscale.

The consideration of randomness in the material geometry (e.g., size, shape, and position of inclusions) and, at the same time, of the physical models of the constituents on the small scale will generate extensive datasets. These datasets serve as the building blocks for further data-driven applications aiming at highly efficient property forecasting and uncertainty quantification of the constitutive response. Machine learning and Artificial Intelligence-based strategies to increase the efficiency of said methods will be probed along with automatic parameter tuning and machine-learned predictors. More systematic but less application-oriented use of our solver technology for stochastically disturbed partial differential equations will be unleashed in cooperation with partnering SimTech groups in the context of Multigrid and Multi-Level Monte Carlo approaches. Thereby, cutting-edge simulation methods are systematically used for data generation. The use of high-fidelity solutions in methodology supported data-driven approaches will eventually lead to notable contributions towards data-integrated simulation science.