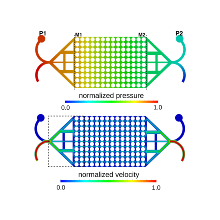
Arndt Wagner, David Krach, Nikolaos Karadimitriou, Paul Voland, Holger Steeb et al. just published their work in Transport in Porous Media:
"Permeability Estimation of Regular Porous Structures: A Benchmark for Comparison of Methods"
Authors
- Arndt Wagner
- Elissa Eggenweiler
- Felix Weinhardt
- Zubin Trivedi
- David Krach
- Christoph Lohrmann
- Kartik Jain
- Nikolaos Karadimitriou
- Carina Bringedal
- Paul Voland
- Christian Holm
- Holger Class
- Holger Steeb
- Iryna Rybak
Abstract
The intrinsic permeability is a crucial parameter to characterise and quantify fluid flow through porous media. However, this parameter is typically uncertain, even if the geometry of the pore structure is available. In this paper, we perform a comparative study of experimental, semi-analytical and numerical methods to calculate the permeability of a regular porous structure. In particular, we use the Kozeny–Carman relation, different homogenisation approaches (3D, 2D, very thin porous media and pseudo 2D/3D), pore-scale simulations (lattice Boltzmann method, Smoothed Particle Hydrodynamics and finite-element method) and pore-scale experiments (microfluidics). A conceptual design of a periodic porous structure with regularly positioned solid cylinders is set up as a benchmark problem and treated with all considered methods. The results are discussed with regard to the individual strengths and limitations of the used methods. The applicable homogenisation approaches as well as all considered pore-scale models prove their ability to predict the permeability of the benchmark problem. The underestimation obtained by the microfluidic experiments is analysed in detail using the lattice Boltzmann method, which makes it possible to quantify the influence of experimental setup restrictions.
Please cite as
A. Wagner, E. Eggenweiler, F. Weinhardt, Z. Trivedi, D. Krach, C. Lohrmann, K. Jain, N. Karadimitriou, C. Bringedal, P. Voland, C. Holm, H. Class, H. Steeb and I. Rybak. Permeability Estimation of Regular Porous Structures: A Benchmark for Comparison of Methods. Transport in Porous Media, 138, 2021, Doi: 10.1007/s11242-021-01586-2