Project image gallery
Participation in Collaborative Research Centers
s.u.
Participation in Priority Programs
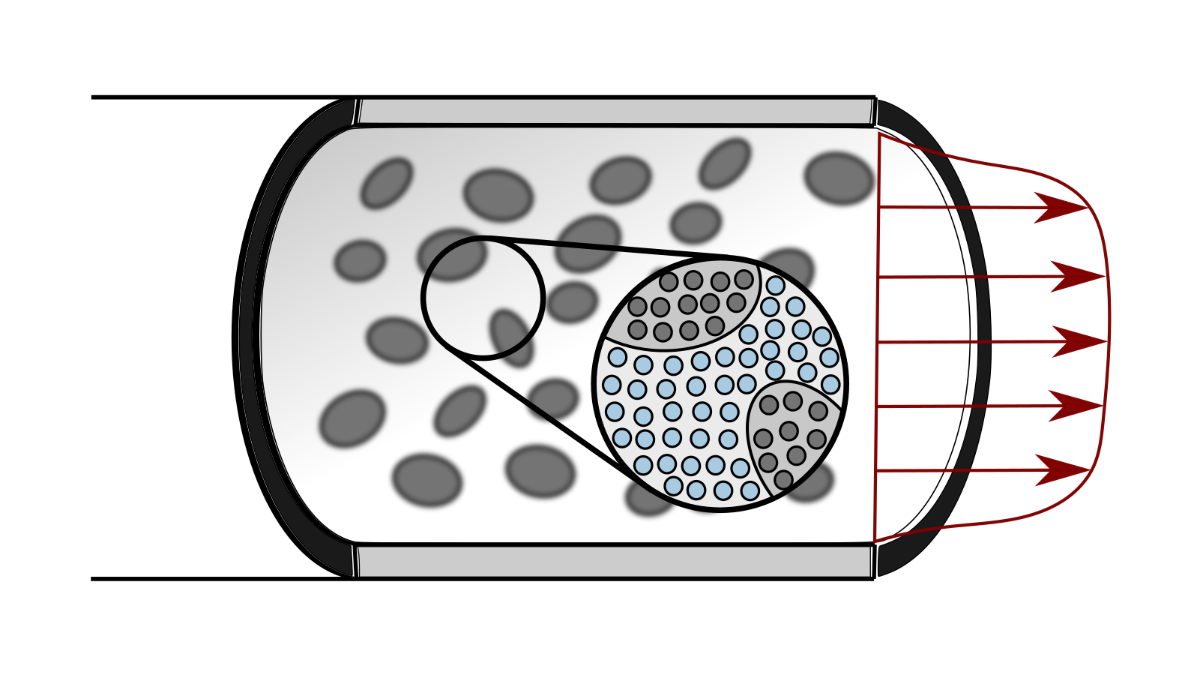
- global aim: Our aim is to model and analyze concrete-like suspensions on multiple scales using microscale-resolved direct numerical simulations. For this purpose, we take advantage of the Lagrangian character of the Smoothed Particle Hydrodynamics (SPH) method to elaborate on the complex motion of single particles.
- keywords: SPH, suspensions, non-Newtonian fluids
- principal investigator: Prof. Dr.-Ing. Holger Steeb
- researcher in charge: Daniel Rostan, M.Sc.
- associated researchers: Nadine Kijanski, M.Sc.; David Krach, M.Sc.
- project identifier: DFG grant No. WI 663 1911/25-1, project No. 386871659
- link to the project website (detailed project description)
Further participations
- global aim: Our aim is to quantify the sensitivity of seismic waves to fracture interconnectivity, in addition to other fracture characteristics, in real fractured rocks by experimental and numerical methods. This includes the optimization of workflows for rock image segmentation and numerical modeling. Another key goal is to strengthen the synergy between the two working groups in the areas of geo-/ rock physics (University of Lausanne) and continuum mechanics (University of Stuttgart).
- keywords: seismic waves, wave attenuation, wave dispersion
- principal investigator of subproject Lausanne: Dr. Beatriz Quintal
- principal investigator of subproject Stuttgart: Prof. Dr.-Ing. Holger Steeb
- researchers of subproject Lausanne: Simón Lissa, M.Sc.; Yury Alkhimenkov, M.Sc.
- researcher in charge of subproject Stuttgart: Matthias Ruf, M.Sc.
- project identifier: DFG grant No. STE 969/13-1, project No. 357361983
- link to the project website (detailed project description)
For further information, please get in touch with the person in charge or alternatively also:

Holger Steeb
Prof. Dr.-Ing.Institute Director
[Image: Holger Steeb]